e-Didaktik am Beispiel Mathematik
Die Beispiele wurden im Rahmen des Fernlernens entwickelt, können aber auch für den Präsenzunterricht verwendet werden.
Unterricht im Fernlernen soll den Lernenden neben dem Üben und Vertiefen auch Zugang zu neuen Themen mit einem strukturierten Aufbau ermöglichen. Wie eine solche Planung und Umsetzung aussehen könnte, wird exemplarisch am Beispiel der Mathematik mit dem Thema „Variablen“ aufgezeigt. Die Einbettung des Aufbaus eines neuen Themas erfolgt dann im Wochen- bzw. Tagesablauf in den verschiedenen vorgesehenen Blöcken.
Die didaktischen Modelle
Basis für die Einführung von neuen Themen bildet im vorliegenden Beispiel das EVTA-Modell, basierend auf dem PADUA-Modell von Hans Aebli, welches einen vollständigen Lernprozess ermöglicht. Es ist vorgesehen, dass für die Umsetzung sowohl digitale Tools wie z.B. OneNote als auch die vorhandenen Lehrmittel verwendet werden. Ein besonderer Fokus gilt der Sicherstellung, dass bei den Lernenden durch die dezentrale Erarbeitung des neuen Themas keine Fehlvorstelllungen entstehen.
Damit auch Nicht-Mathematik-Lehrpersonen der Transfer ins eigene Unterrichtsgebiet gelingt, sind unter „Grundlegende Überlegungen“ Hintergrundinformationen zur Fachdidaktik Mathematik im Fernlernen sowie inhaltlich zum Thema „Variablen“ vorhanden.
↓ Die didaktischen Modelle EVTA und PADUA
Das Lernen von Mathematik folgt im Fernunterricht grundsätzlich denselben lerntheoretischen Prinzipien wie im Präsenzunterricht in der Schule. Das Mathematiklehrmittel der Sekundarstufe I stützt sich mit dem EVTA-Modell auf den Ansatz von Hans Aeblis PADUA-Modell. Auch für die weiteren Überlegungen für die Mathematik auf der Primarstufe wird das EVTA-Modell verwendet.
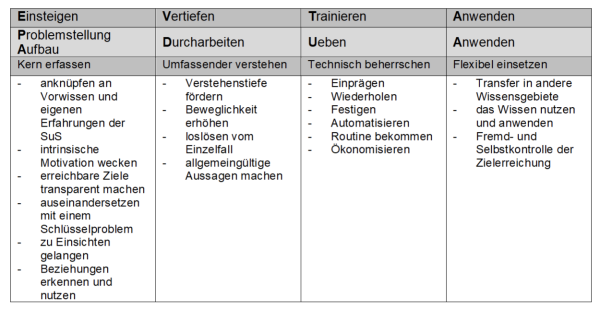
Eine Einleitung zum PADUA-Modell findet sich in: Krieg, Martina und Kurt Hess. 2017. «Strukturieren nach dem PADUA-Modell.» In Kompetenzorientierter Unterricht: Orientierung, 18-19. Zug: Direktion für Bildung und Kultur. Es wird eine PDF-Datei gespeichert.
Die einzelnen Phasen werden nicht linear durchlaufen, es kommt auch immer wieder zu Schleifen. Während in den Phasen des Einsteigens und Vertiefens hauptsächlich mit dem Themenbuch gearbeitet wird, finden sich die Aufgaben für das Trainieren sowohl im Arbeitsheft wie auch in den Onlinetrainern. Bei der Erarbeitung eines Themas wird oft zwischen dem Themenbuch und dem Arbeitsheft hin- und hergewechselt. So kann dann der Ablauf der einzelnen Phasen wie folgt aussehen: E-V-T-V-T-V-T-A.
Wichtig dabei ist, dass das Trainieren (Automatisieren, Festigen) erst erfolgt, wenn ein Verständnis aufgebaut wurde.
Zusammengefasst lässt sich sagen, dass das EVTA-Modell ein Modell ist, welches
- einen vollständigen Lernprozess beschreibt,
- Faktoren beschreibt, welche diesen Prozess positiv beeinflussen und
- aufzeigt, wie die Lehrperson eine Lernsequenz entwerfen, strukturieren und gestalten und damit einen vollständigen Lernprozess unterstützen kann.
Grundidee von Aebli: Wenn die Lernenden den Lernprozess vollständig durchlaufen, dann haben sie die Chance, das Gelernte auch wirklich zu verinnerlichen und nicht mehr zu vergessen.
↓ Das ACAT-Modell
Beim Fernlernen bekommen digitale Hilfsmittel eine tragende Rolle. Um den Einsatz von digitalen Artefakten einordnen zu können, bietet das ACAT-Modell (Artefact Centric Activitiy Theory,) von Silke Ladel und Ulrich Kortenkamp einen theoretischen Rahmen. Das ACAT-Modell fand ursprünglich seine Anwendung bei der Beurteilung von Apps im Mathematikunterricht, es lässt sich aber auch auf digitale Hilfsmittel im Allgemeinen erweitern.
Eine gute Einleitung zum ACAT-Modell und deren Nutzen für die Beurteilung von Apps im Mathematikunterricht findet sich hier:
Etzold, Heiko, Ulrich Kortenkamp und Silke Ladel. 2018. «ACAT-Review-Guide - Ein tätigkeitstheoretischer Blick auf die Beurteilung von Mathematik-Apps.» In Mathematik mit digitalen Medien - konkret. Ein Handbuch für Lehrpersonen der Primarstufe. Münster: WTM-Verlag.
Grundlegende Bemerkungen zur Umsetzung
Eine konkrete Umsetzung des Mathematikunterrichts im Fernlernen findet an einem Beispiel aus der 6. Primar (Kapitel «Gleichungen und Unbekannte») und aus der 1. Sekundarklasse (Kapitel «8a Terme und Termumformungen») statt. Dazu werden die einzelnen Beiträge in einem Fernlernplan (6. Klasse, 1. Sek) zusammengestellt. Diese Dokumente wie auch alle anderen zur Verfügung gestellten Dokumente (siehe 5.6 und 6.4) sind so einfach wie möglich formatiert, sodass leicht eigene Anpassungen im Inhalt wie auch im Layout gemacht werden können.
↓ Digitales Arbeiten
Im Fernlernpass wird regelmässig erwähnt, dass die Schülerinnen und Schüler die Lösungen in ihr Matheheft schreiben sollen. In der Zeit des Fernlernens hat dies den Nachteil, dass die Schülerinnen und Schüler nur mit Hilfe von Lösungsvorlagen ihre Lösungen selbst korrigieren können. Wenn es die technische Infrastruktur erlaubt, sind für das Fernlernen folgende digitale Lösungen vorteilhaft:
- Die Klasse arbeitet mit einem digitalen Notizbuch (z.B. OneNote). Dort können die Schülerinnen und Schüler ihre Lösungen hineinschreiben (auch direkt handschriftlich oder mit Fotos von handschriftlich verfassten Lösungen). Ebenso können die Word-Dokumente welche in diesem Fernlernpass genutzt werden direkt in das Notizbuch als «Ausdruck» eingefügt werden. So hat die Lehrperson einen Einblick in den Lernfortschritt der Schülerinnen und Schüler und kann allenfalls Fehlvorstellungen frühzeitig erkennen.
- Alternativ kann auch mit Word-Dokumenten gearbeitet werden, welche auf einem Onlinespeicher der Schule abgelegt werden. Hier ist es für die Lehrperson auch möglich, Einblick in die Dokumente zu erlangen, jedoch ist das Vorgehen etwas komplizierter als in einem digitalen Notizbuch.
Erweiterte Formen wie ein Learning Management System (LMS) werden hier nicht genutzt. Lehrpersonen, welche bereits ein solches LMS verwenden, können die Aufträge leicht in die entsprechende Form bringen.
Variablen - Bedeutung und Hinweise
Variablen haben zwei Bedeutungen:
Die Variable steht für einen unbekannten Wert: In einer Gleichung wie «3 + x = 10» steht die Variable für eine Zahl, welche zwar aktuell unbekannt ist, jedoch eindeutig bestimmt werden kann.
Die Variable steht für einen variablen Wert: In Formeln und Termen wie «Gesamtpreis = 3x» steht das x zum Beispiel für den Preis einer Einheit (z.B. Preis eines Apfels). Für die Variable x kann variabel der jeweils entsprechende Preis eingesetzt und so der Gesamtpreis ausgerechnet werden.
Gerade beim Fernlernen nehmen allfällige Fehlvorstellungen eine wichtige Rolle ein. Fehlvorstellungen sind dann besonders problematisch, wenn die Schülerinnen und Schüler in den ersten Aufgaben noch zu (meist) korrekten Resultaten gelangen und die Fehlvorstellung so noch gar nicht zum Tragen kommt, sondern sich sogar noch festigt.
Mögliche Umsetzung auf der Primarstufe
Entlang des EVTA-Modells wird die konkrete Umsetzung des Themas „Gleichungen und Unbekannte“ im Fernlernen aufgezeigt. Die einzelnen Phasen werden beschrieben und die didaktischen Hintergründe erläutert. Am Schluss findet sich ein Fernlernplan mit Verlinkungen.
↓ Phase «Einsteigen»
Beim Einstieg wird an das Vorwissen der Schülerinnen und Schüler angeknüpft. Um bestehende Konzepte erweitern zu können, müssen zum einen die bestehenden Konzepte selbst wie auch die möglichen Schwierigkeiten beim Erweitern bekannt sein.
In der 5. Primarklasse wird das Thema «Terme und Gleichungen» bereits aufgegriffen. Dort werden auch die grauen Boxen als Repräsentant für eine unbekannte Zahl eingeführt, ohne dass der Begriff «Unbekannte» selbst verwendet wird. Dieses Konzept wird von der 1. Klasse an spiralförmig aufgebaut (vgl. Mathematik 1 Primar, Handbuch Seite 233; Mathematik 3 Primar, Themenbuch Seite 93; Mathematik 4 Primar, Themenbuch Seite 93).
In «Mathematik 5 Primarstufe» und in «Mathematik Primar 6» werden Gleichungen und Ungleichungen experimentell und mithilfe von Rechenbäumen gelöst. Umformungen im algebraischen Sinn sind nicht das Ziel, sondern vielmehr Fragen wie «Welche Zahl muss ich zu 700 addieren, um 1260 zu erhalten?». Dabei spielen auch die Umkehroperationen eine wichtige Rolle. Als Vorstufe zu algebraischen Umformungen wird von Anfang an immer wieder das Konzept «3 Zahlen und 4 Gleichungen» thematisiert (vgl. Mathematik 1 Primar, Handbuch Seite 215; Mathematik 3 Primar, Themenbuch Seite 65; Mathematik 4 Primar, Themenbuch Seite 93 oben; Mathematik 6 Primar, Themenbuch Seite 108 oben).
↓ Phase «Vertiefen»
Die Phasen des Einsteigens und des Vertiefens sind auf der Primarstufe nicht klar abgegrenzt. Es findet aber dennoch ein Abstraktionsprozess statt. Während bei der Aufgabe 2 (siehe Unterstützungsmaterial) der Fokus noch mehr auf der Variablen liegt und die Zahl rechts vom Gleichheitszeichen noch als Resultat der Rechnung auf der linken Seite aufgefasst werden kann, wird mit der Aufgabe 3 das Konzept der Gleichung fokussiert, nämlich das links und rechts des Gleichheitszeichens zwei Terme stehen, welche ausgerechnet das selbe Resultat haben. Dies wird nun bei der Aufgabe 4 aufgegriffen, indem zuerst eine Seite der Gleichung ausgerechnet werden muss, bevor die Unbekannte bestimmt werden kann. Mit der Aufgabe 5 kommen Terme mit zwei Operationszeichen hinzu. Als Lösungsmethoden werden ein Rechenbaum oder das schrittweise Umformen der Gleichung vorgeschlagen.
↓ Phase «Trainieren»
Bevor es zum Automatisieren in der Trainingsphase kommt, wird im Fernlernpass jeweils (ausser bei der Aufgabe 1) bei den «Grundlagen für alle» eine formative Lernzielkontrolle vorgeschaltet.
Innerhalb der Trainingsphase werden einzelne Aufgaben direkt von den Schülerinnen und Schülern selbst korrigiert. Diese Lösungen müssen in geeigneter Weise zur Verfügung gestellt werden. Gleichzeitig werden einige Aufgabe aus dem Arbeitsheft zur Diagnose genutzt. Diese Aufgaben werden der Lehrperson zur Korrektur geschickt. Es wurde darauf geachtet, dass die gewählten Aufgaben genügend Diagnosepotential haben, sodass die Lehrperson Einblicke in die Lernstände der Schülerinnen und Schüler bekommen kann und allenfalls durch Telefongespräche eine tiefergehende Diagnose durchführen oder auch geeignete Hilfestellungen geben kann.
↓ Phase «Anwenden»
In die Anwendungsphase gehören einerseits Transferaufgaben wie auch die Leistungsüberprüfung. Da das Thema «Gleichungen und Unbekannte» das letzte Kapitel zum Bereich «Rechenoperationen» ist, findet der Transfer erst in der Sekundarstufe I statt, wenn mit dem Kapitel «2b Variablen» das Konzept der Unbekannten wieder aufgegriffen und erweitert wird, indem zum einen Buchstaben anstelle der Platzhalter verwendet werden, zum andern aber auch tiefgreifender die Variablen neu auch die Bedeutung des variablen bekommen.
Auf eine summative Überprüfung des Gelernten wird hier verzichtet.
↓ Unterstützungsmaterial
Fernlernplan für die Primarstufe mit aktiven Verlinkungen.
Mögliche Umsetzung für die Sekundarstufe I
Entlang des EVTA-Modells wird die konkrete Umsetzung des Themas „Variablen“ im Fernlernen aufgezeigt. Die einzelnen Phasen werden beschrieben und die didaktischen Hintergründe erläutert. Im Register «Unterstützungsmaterialien» findet sich der Fernlernlernplan mit Verlinkungen und Verweisen zu weiteren Materialien für die Umsetzung des Themas im Fernlernen.
↓ Phase «Einsteigen»
Beim Einstieg wird an das Vorwissen der Schülerinnen und Schüler angeknüpft. Um bestehende Konzepte erweitern zu können, müssen zum einen die bestehenden Konzepte selbst wie auch die möglichen Schwierigkeiten beim Erweitern bekannt sein.
Die Definition einer Variablen im Begleitheft beim vorausgehenden Kapitel 2b kann zu einer Fehlvorstellung führen und sollte daher zwingend thematisiert werden: «Eine Variable wird mit einem Buchstaben notiert. Statt diesem Buchstaben kannst du grundsätzlich irgendeine Zahl setzen; in einem Term steht er für irgendeinen Wert.» (Begleitheft Mathematik 1, Kapitel 2b, Seite 30).
Im Kapitel 8a heisst es ähnlich: «Du kannst in einem Term anstelle einer Variablen eine beliebige Zahl einsetzen.» (Begleitheft Mathematik 1, Kapitel 8a, Seite 96).
Diese beiden Definitionen sind nicht falsch, treffen aber nur zu, wenn man Variablen in einer Funktion oder in einer Formel verwendet. Bei den im Kapitel 8b folgenden Gleichungen sind diese Definitionen jedoch problematisch, da bei Gleichungen die Variable nicht für eine beliebige Zahl steht, sondern für eine noch unbekannte Zahl, welche man bestimmen kann.
Bezug zur Primarstufe: Im Lehrmittel «Mathematik 6 Primar» (Kapitel «Gleichungen und Unbekannte») werden die Variablen eingeführt, wobei hier der Begriff «Unbekannte» verwendet wird. Dieser Begriff ist zutreffend, da hier Variablen immer im Kontext von Gleichungen erscheinen und auch noch nicht mit Buchstaben abgekürzt werden, sondern mit grauen Kästchen. Handelnd wird das Prinzip der unbekannten Zahl auch so dargestellt, dass in einer Gleichung eine Zahl durch eine Haftnotiz abgedeckt wird.
Der Einstieg in das Thema «Rechnen mit Variablen» auf der Sekundarstufe I geschieht über Situationen im Restaurant, in welchem zwei Menüs angeboten werden. Dabei ist zu beachten, dass die Schülerinnen und Schüler nicht die Fehlvorstellung aufbauen, dass die Variablen p und f jeweils für die Menüs selbst stehen. Bei den Restaurantaufgaben geht es zum einen darum, Sachsituationen mit Hilfe von Variablen und Termen darzustellen (Terme bilden, «vom Text zum Term»), zum andern auch um die umgekehrte Richtung, algebraische Terme situationsbezogen zu beschreiben (Terme interpretieren, «vom Term zum Text»).
↓ Phase «Vertiefen»
Der Übergang von Einsteigen zum Vertiefen findet fliessend statt. Beim Vertiefen löst man sich immer mehr von Spezialfall des Einstiegs. Auch wenn bis zur Aufgabe 5 die Aufgaben stets der Bezug zum Restaurant bleibt, werden die Aufgaben immer abstrakter. Es ist jedoch wichtig, dass immer noch der Bezug zu einer realen Situation gemacht werden kann. Erst ab Aufgabe 6 ist die Variable ein rein abstrakter Gegenstand, welcher zwar noch durch die Seitenlängen repräsentiert wird. Bei der Arbeit mit den Kärtchen steht jedoch mehr das Herleiten und die Überprüfung der Rechenregeln im Vordergrund als der Aufbau der Grundvorstellungen zum Variablen-Konzept.
Am Ende der Vertiefungsphase folgt jeweils der Verweis auf das Begleitheft.
↓ Phase «Trainieren»
Bevor es zum Automatisieren in der Trainingsphase kommt, wird im Fernlernpass jeweils eine formative Lernzielkontrolle vorgeschaltet.
Innerhalb der Trainingsphase werde einzelne Aufgaben direkt von den Schülerinnen und Schülern selbst korrigiert. Diese Lösungen müssen in geeigneter Weise zur Verfügung gestellt werden. Gleichzeitig werden einige Aufgabe aus dem Arbeitsheft zur Diagnose genutzt. Diese Aufgaben werden der Lehrperson zur Korrektur geschickt. Es wurde darauf geachtet, dass die gewählten Aufgaben genügend Diagnosepotential haben, sodass die Lehrperson Einblicke in die Lernstände der Schülerinnen und Schüler bekommen kann und allenfalls durch Telefongespräche eine tiefergehende Diagnose durchführen kann, oder auch geeignete Hilfestellungen geben kann.
↓ Phase «Anwenden»
In die Anwendungsphase gehören einerseits Transferaufgaben wie auch die Leistungsüberprüfung. Der Transfer findet anschliessend im Kapitel 8b statt, wenn die aufgebauten Kompetenzen zur Termumformung genutzt werden können, um Gleichungen zu lösen. Dafür ist dann auch ein gutes konzeptionelles Wissen zu den Variablen notwendig.
Auf eine summative Überprüfung des Gelernten wird hier verzichtet.